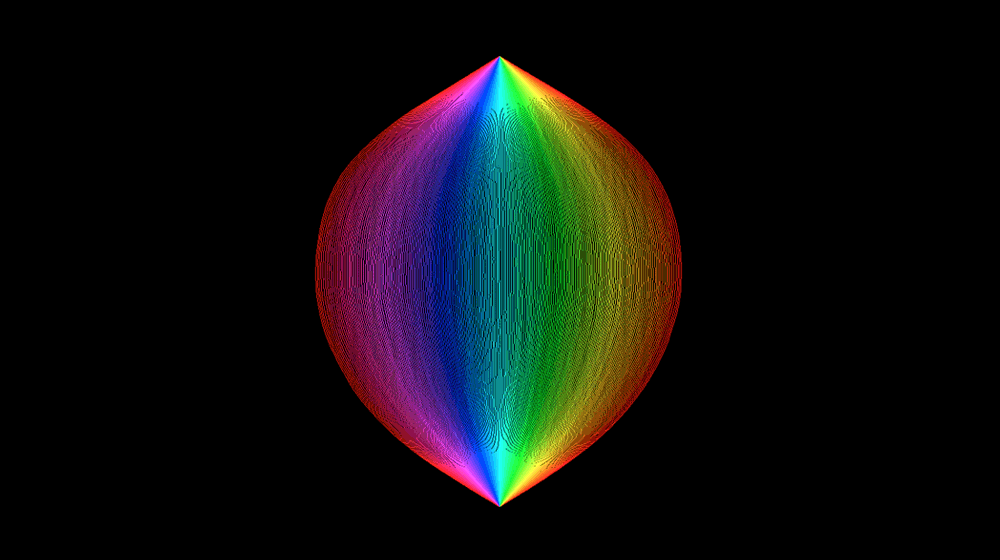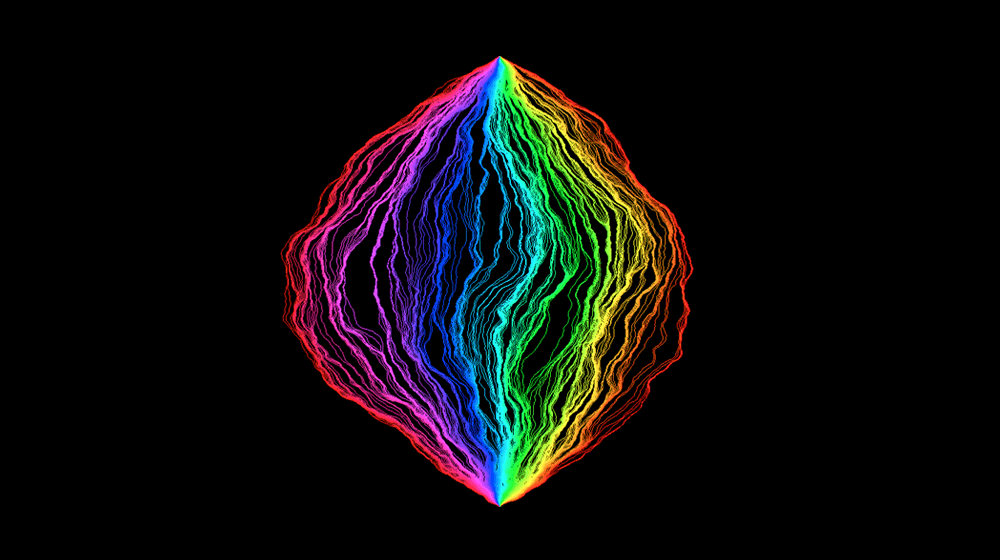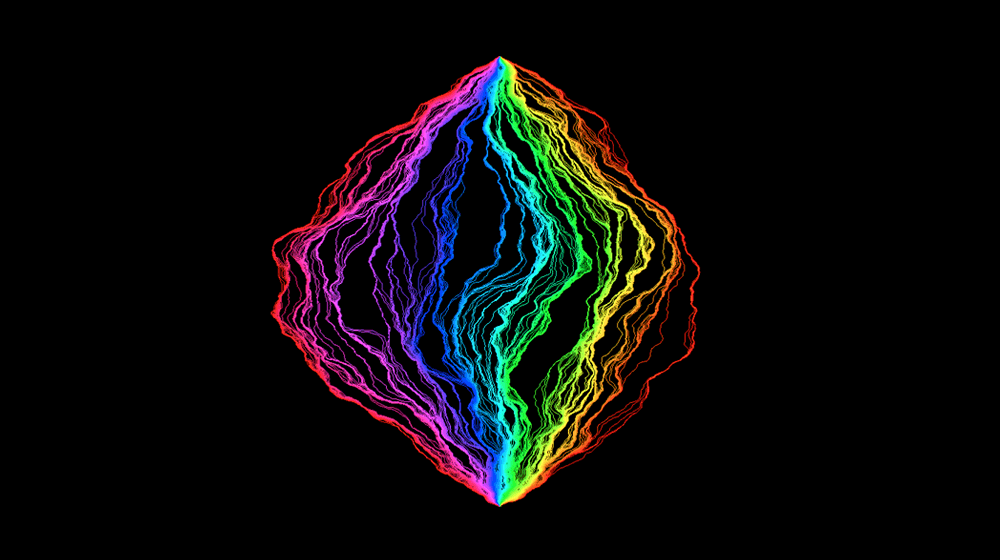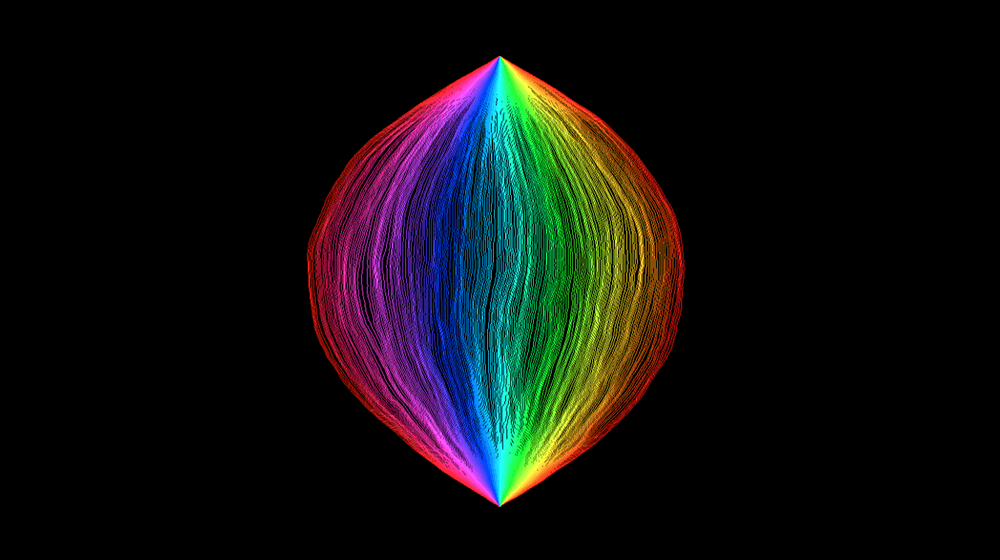
Researchers have uncovered deep connections among different types of random objects, illuminating hidden geometric structures.
Standard geometric objects can be described by simple rules — every straight line, for example, is just y = ax + b — and they stand in neat relation to each other: Connect two points to make a line, connect four line segments to make a square, connect six squares to make a cube.
These are not the kinds of objects that concern Scott Sheffield.
Ref: Liouville quantum gravity and the Brownian map II: geodesics and continuity of the embedding. arXiv - Mathematics > Probability (11 May 2016) | arXiv.org/abs/1605.03563
ABSTRACT
We endow the √8/3-Liouville quantum gravity sphere with a metric space structure and show that the resulting metric measure space agrees in law with the Brownian map. Recall that a Liouville quantum gravity sphere is a priori naturally parameterized by the Euclidean sphere S2. Previous work in this series used quantum Loewner evolution (QLE) to construct a metric dQ on a countable dense subset of S2. Here we show that dQ a.s. extends uniquely and continuously to a metric dQ on all of S2. Letting d denote the Euclidean metric on S2, we show that the identity map between (S2,d) and (S2,d¯Q) is a.s. H\"older continuous in both directions. We establish several other properties of (S2,d¯Q), culminating in the fact that (as a random metric measure space) it agrees in law with the Brownian map. We establish analogous results for the Brownian disk and plane. Our proofs involve new estimates on the size and shape of QLE balls and related quantum surfaces, as well as a careful analysis of (S2,d¯Q) geodesics.